String theory is one of the most exciting and profound developments in modern theoretical physics. Unfortunately it is a highly technical subject that can only be well understood using the tools of Quantum Field Theory and General Relativity. It also doesn't hurt to know some mathematics like Group Theory, Differential Geometry, and Algebraic Geometry. Needless to say this is prohibitive for most people who are far too busy doing other things.
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings. It is considered one of the most promising candidate theories of quantum gravity. Superstring theory is a shorthand for supersymmetric string theory because unlike bosonic string theory, it is the version of string theory that incorporates fermions and supersymmetry.
Why Strings?
So, what is the world made of? Ordinary matter is made of atoms, which are in turn made of just three basic components: electrons whirling around a nucleus composed of neutrons and protons. The electron is a truly fundamental particle (it is one of a family of particles known as leptons), but neutrons and protons are made of smaller particles, known as quarks. Quarks are, as far as we know, truly elementary.
Our current knowledge about the subatomic composition of the universe is summarized in what is known as the Standard Model of particle physics. It describes both the fundamental building blocks out of which the world is made, and the forces through which these blocks interact. There are twelve basic building blocks. Six of these are quarks--- they go by the interesting names of up, down, charm, strange, bottom and top. (A proton, for instance, is made of two up quarks and one down quark.) The other six are leptons--- these include the electron and its two heavier siblings, the muon and the tauon, as well as three neutrinos.
There are four fundamental forces in the universe: gravity, electromagnetism, and the weak and strong nuclear forces. Each of these is produced by fundamental particles that act as carriers of the force. The most familiar of these is the photon, a particle of light, which is the mediator of electromagnetic forces. (This means that, for instance, a magnet attracts a nail because both objects exchange photons.) The graviton is the particle associated with gravity. The strong force is carried by eight particles known as gluons. Finally, the weak force is transmitted by three particles, the W+, the W- , and the Z.
The behavior of all of these particles and forces is described with impeccable precision by the Standard Model, with one notable exception: gravity. For technical reasons, the gravitational force, the most familiar in our every day lives, has proven very difficult to describe microscopically. This has been for many years one of the most important problems in theoretical physics-- to formulate a quantum theory of gravity.
In the last few decades, string theory has emerged as the most promising candidate for a microscopic theory of gravity. And it is infinitely more ambitious than that: it attempts to provide a complete, unified, and consistent description of the fundamental structure of our universe. (For this reason it is sometimes, quite arrogantly, called a 'Theory of Everything').
The essential idea behind string theory is this: all of the different 'fundamental ' particles of the Standard Model are really just different manifestations of one basic object: a string. How can that be? Well, we would ordinarily picture an electron, for instance, as a point with no internal structure. A point cannot do anything but move. But, if string theory is correct, then under an extremely powerful 'microscope' we would realize that the electron is not really a point, but a tiny loop of string. A string can do something aside from moving--- it can oscillate in different ways. If it oscillates a certain way, then from a distance, unable to tell it is really a string, we see an electron. But if it oscillates some other way, well, then we call it a photon, or a quark, or a ... you get the idea. So, if string theory is correct, the entire world is made of strings!
Perhaps the most remarkable thing about string theory is that such a simple idea works--- it is possible to derive (an extension of) the Standard Model (which has been verified experimentally with incredible precision) from a theory of strings. But it should also be said that, to date, there is no direct experimental evidence that string theory itself is the correct description of Nature. This is mostly due to the fact that string theory is still under development. We know bits and pieces of it, but we do not yet see the whole picture, and we are therefore unable to make definite predictions. In recent years many exciting developments have taken place, radically improving our understanding of what the theory is.
While the Standard Model has been very successful in describing most of the phenomemon that we can experimentally investigate with the current generation of particle acceleraters, it leaves many unanswered questions about the fundamental nature of the universe. The goal of modern theoretical physics has been to find a "unified" description of the universe. This has historically been a very fruitful approach. For example Einstein-Maxwell theory unifies the forces of electricity and magnetism into the electromagnetic force. The Nobel prize winning work of Glashow, Salam, and Weinberg successfully showed that the electromagnetic and weak forces can be unified into a single electroweak force. There is actually some pretty strong evidence that the forces of the Standard Model should all unify as well. When we examine how the relative strengths of the strong force and electroweak force behave as we go to higher and higher energies, we find that they become the same at an energy of about 10^16 GeV. In addition the gravitational force should become equally important at an energy of about 10^19 GeV.
The goal of string theory is to explain the "?" in the above diagram.
The characteristic energy scale for quantum gravity is called the Planck Mass, and is given in terms of Planck constant, the speed of light, and Newton's constant,
Physics at this high energy scale describes the universe as it existed during the first moments of the Big Bang. These high energy scales are completely beyond the range which can be created in the particle accelerators we currently have (or will have in the foreseeable future.) Most of the physical theories that we use to understand the universe that we live in also break down at the Planck scale. However, string theory shows unique promise in being able to describe the physics of the Planck scale and the Big Bang.
In its final form string theory should be able to provide answers to answer questions like:
• Where do the four forces that we see come from?
• Why do we see the various types of particles that we do?
• Why do particles have the masses and charges that we see?
• Why do we live in 4 spacetime dimensions?
• What is the nature of spacetime and gravity?
String Basics
We are used to thinking of fundamental particles (like electrons) as point-like 0-dimensional objects. A generalization of this is fundamental strings which are 1-dimensional objects. They have no thickness but do have a length, typically 10-33 cm [that's a decimal point followed by 32 zeros and a 1]. This is very small compared to the length scales that we can reasonably measure, so these strings are so small that they practically look like point particles. However their stringy nature has important implications as we will see.
Strings can be open or closed. As they move through spacetime they sweep out an imaginary surface called a worldsheet.
These strings have certain vibrational modes which can be characterized by various quantum numbers such as mass, spin, etc. The basic idea is that each mode carries a set of quantum numbers that correspond to a distinct type of fundamental particle. This is the ultimate unification: all the fundamental particles we know can be described by one object, a string! [A very loose analogy can be made with say, a violin string. The vibrational modes are like the harmonics or notes of the violin string, and each type of particle corresponds to one of these notes.]
As an example let's consider a closed string mode which looks like:
This mode is characteristic of a spin-2 massless graviton (the particle that mediates the force of gravity). This is one of the most attractive features of string theory. It naturally and inevitably includes gravity as one of the fundamental interactions.
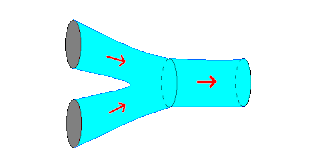
Strings interact by splitting and joining. For example the anihilation of two closed strings into a single closed string occurs with a interaction that looks like:
Notice that the worldsheet of the interaction is a smooth surface. This essentially accounts for another nice property of string theory. It is not plagued by infinities in the way that point particle quantum field theories are. The analogous Feynman diagram in a point particle field theory is:
Notice that the interaction point occurs at a topological singularity in the diagram (where the 3 world-lines intersect). This leads to a break down of the point particle theory at high energies.
If we glue two of the basic closed string interactions together, we get a process by which two closed strings interact by joining into an intermediate closed string which splits apart into two closed strings again:
The nice thing about this is that at each order in perturbation theory there is only one diagram. [In point particle field theories the number of diagrams grows exponentially at higher orders.] The bad news is that extracting answers from diagrams with more than about two handles is very difficult due to the complexity of the mathematics involved in dealing with these surfaces. Perturbation theory is a very useful tool for studying the physics at weak coupling, and most of our current understanding of particle physics and string theory is based on it. However it is far from complete. The answers to many of the deepest questions will only be found once we have a complete non-perturbative description of the theory.
Extra Dimensions
Superstrings live in a 10-dimensional spacetime, but we observe a 4-dimensional spacetime. Somehow we need to link the two if superstrings are to describe our universe. To do this we curl up the extra 6 dimensions into a small compact space. If the size of the compact space is of order the string scale (10-33 cm) we wouldn't be able to detect the presence of these extra dimensions directly - they're just too small. The end result is that we get back to our familiar (3+1)-dimensional world, but there is a tiny "ball" of 6-dimensional space associated with every point in our 4-dimensional universe. This is shown in an extremely schematic way in the following illustration:
This is actually a very old idea dating back to the 1920's and the work of Kaluza and Klein. This mechanism is often called Kaluza-Klein theory or compactification. In the original work of Kaluza it was shown that if we start with a theory of general relativity in 5-spacetime dimensions and then curl up one of the dimensions into a circle we end up with a 4-dimensional theory of general relativity plus electromagnetism! The reason why this works is that electromagnetism is a U(1) gauge theory, and U(1) is just the group of rotations around a circle. If we assume that the electron has a degree of freedom corresponding to point on a circle, and that this point is free to vary on the circle as we move around in spacetime, we find that the theory must contain the photon and that the electron obeys the equations of motion of electromagnetism (namely Maxwell's equations). The Kaluza-Klein mechanism simply gives a geometrical explanation for this circle: it comes from an actual fifth dimension that has been curled up. In this simple example we see that even though the compact dimensions maybe too small to detect directly, they still can have profound physical implications. [Incidentally the work of Kaluza and Klein leaked over into the popular culture launching all kinds of fantasies about the "Fifth dimension"!]
How would we ever really know if there were extra dimensions and how could we detect them if we had particle accelerators with high enough energies? From quantum mechanics we know that if a spatial dimension is periodic the momentum in that dimension is quantized, p = n / R (n=0,1,2,3,....), whereas if a spatial dimension is unconstrained the momentum can take on a continuum of values. As the radius of the compact dimension decreases (the circle becomes very small) then the gap between the allowed momentum values becomes very wide. Thus we have a Kaluza Klein tower of momentum states.
If we take the radius of the circle to be very large (the dimension is de-compactifying) then the allowed values of the momentum become very closely spaced and begin to form a continuum. These Kaluza-Klein momentum states will show up in the mass spectrum of the uncompactifed world. In particular, a massless state in the higher dimensional theory will show up in the lower dimensional theory as a tower of equally spaced massive states just as in the picture shown above. A particle accelerator would then observe a set of particles with masses equally spaced from each other. Unfortunately, we'd need a very high energy accelerator to see even the lightest massive particle.
Strings have a fascinating extra property when compactified: they can wind around a compact dimension which leads to winding modes in the mass spectrum. A closed string can wind around a periodic dimension an integral number of times. Similar to the Kaluza-Klein case they contribute a momentum which goes as p = w R (w=0,1,2,...). The crucial difference here is that this goes the other way with respect to the radius of the compact dimension, R. So now as the compact dimension becomes very small these winding modes are becoming very light!
Now to make contact with our 4-dimensional world we need to compactify the 10-dimensional superstring theory on a 6-dimensional compact manifold. Needless to say, the Kaluza Klein picture described above becomes a bit more complicated. One way could simply be to put the extra 6 dimensions on 6 circles, which is just a 6-dimensional Torus. As it turns out this would preserve too much supersymmetry. It is believed that some supersymmetry exists in our 4-dimensional world at an energy scale above 1 TeV (this is the focus of much of the current and future research at the highest energy accelerators around the word!). To preserve the minimal amount of supersymmetry, N=1 in 4 dimensions, we need to compactify on a special kind of 6-manifold called a Calabi-Yau manifold.
The properties of the Calabi-Yau manifold can have important implications for low energy physics such as the types of particles observed, their masses and quantum numbers, and the number of generations. One of the outstanding problems in the field has been the fact that there are many many Calabi-Yau manifolds (thousands upon thousands?) and we have no way of knowing which one to use. In a sense we started with a virtually unique 10-dimensional string theory and have found that possibilities for 4-dimensional physics are far from unique, at least at the level of our current (and incomplete) understanding. The long-standing hope of string theorists is that a detailed knowledge of the full non-perturbative structure of the theory, will lead us to an explanation of how and why our universe flowed from the 10-dimensional physics that probably existed during the high energy phase of the Big Bang, down to the low energy 4-dimensional physics that we observe today. [Possibly we will find a unique Calabi-Yau manifold that does the trick.] Some important work of Andrew Strominger has shown that Calabi-Yau manifolds can be continuously connected to one another through conifold transitions and that we can move between different Calabi-Yau manifolds by varying parameters in the theory. This suggests the possibility that the various 4-dimensional theories arising from different Calabi-Yau manifolds might actually be different phases of an single underlying theory.
Black Holes
The classical description of gravity known as General Relativity, contains solutions which are called "black holes". There are many different kinds of black hole solutions but they share some common characteristics. The event horizon is a surface in spacetime which, loosely speaking, divides the inside of the black hole from the outside. The gravitational attraction of a black hole is so strong that any object that crosses the event horizon, including light, can never escape out of the black hole. Classical black holes are therefore relatively featureless, but they can be described by a set of observable parameters such as mass, charge, and angular momentum.
Black holes turn out to be important "laboratories" in which to test string theory, because the effects of quantum gravity turn out to be important even for large macroscopic holes. Black holes aren't really "black" since they radiate! Using semi-classical reasoning, Stephen Hawking showed black holes emit a thermal spectrum of radiation at their event horizon. Since string theory is, among other things, a theory of quantum gravity, it should be able to describe black holes in a consistent way. In fact there are black hole solutions which satisfy the string equations of motion. These equations of motion resemble the equations of general relativity with some extra matter fields coming from string theory. Superstring theories also have some special black hole solutions which are themselves supersymmetric, in that they preserve some supersymmetry.
One of the most dramatic recent results in string theory is the derivation of the Bekenstein-Hawking entropy formula for black holes obtained by counting the microscopic string states which form a black hole. Bekenstein noted that black holes obey an "area law", dM = K dA, where 'A' is the area of the event horizon and 'K' is a constant of proportionality. Since the total mass 'M' of a black hole is just its rest energy, Bekenstein realized that this is similar to the thermodynamic law for entropy, dE = T dS. Hawking later performed a semiclassical calculation to show that the temperature of a black hole is given by T = 4 k [where k is a constant called the "surface gravity"]. Therefore the entropy of a black hole should be written as S = A/4. Physicists Andrew Strominger and Cumrin Vafa, showed that this exact entropy formula can be derived microscopically (including the factor of 1/4) by counting the degeneracy of quantum states of configurations of strings and D-branes which correspond to black holes in string theory. This is compelling evidence that D-branes can provide a short distance weak coupling description of certain black holes! For example, the class of black holes studied by Strominger and Vafa are described by 5-branes, 1-branes and open strings traveling down the 1-brane all wrapped on a 5-dimensional torus, which gives an effective one dimensional object -- a black hole.
Hawking radiation can also be understood in terms of the same configuration, but with open strings traveling in both directions. The open strings interact, and radiation is emitted in the form of closed strings. The system decays into the configuration shown above.
Explicit calculations show that for certain types of supersymmetric black holes, the string theory answer agrees with the semi-classical supergravity answer including non-trivial frequency dependent corrections called greybody factors. This is more evidence that string theory is a consistent and accurate fundamental theory of quantum gravity.
Summary
Superstring theory is a very exciting area of study because it has the serious potential to be the right theory for describing the fundamental nature of our universe. All the elements are in there: quantum physics, bosons, fermions, gauge groups, and gravity. In the last several years there has been great progress in understanding the overall structure of the theory including D-branes and string duality. String theory has been applied with great success to the study of black hole physics and quantum gravity. However, there is much work yet to be done.
No comments:
Post a Comment